How To Find The Moment Of Inertia For Composite Shapes

Moment of Inertia of composite shapes

Home > Resources > Finding the moment of inertia of composite shapes

Table of contents

Process outline

The given analytical formulas for the calculation of moments of inertia usually cover, simply a handful of rather simple cases. The possible shape geometries one may encounter however, are unlimited, but most of the times, these complex areas tin can be decomposed to more than uncomplicated subareas. In this article, it is demonstrated how to calculate the moment of inertia of complex shapes, using the Parallel Axes Theorem.

In general, the steps for the calculation of the moment of inertia of a composite area, around an axis (chosen global centrality hereafter), are summarized to the following:

1. Identify simply shaped subareas the blended area tin exist decomposed to.
2. Determine the altitude from global centrality of the centroid of each one of the subareas.
3. Determine the moment of inertia of each subarea, effectually a parallel axis, passing through subarea centroid.
4. Apply the Parallel Axes Theorem to find the moment of inertia of each subarea around the global axis.
5. Add (or subtract for negative subareas, see examples) the moments of inertia from the last step.

Figure ane. Flowchart for the adding of the moment of inertia of a blended expanse

With step 1 we aim to divide the complex area under investigation to smaller and more manageable subareas. While doing so, we must ensure that nosotros can efficiently obtain the moment inertia of each subarea, around a parallel axis. Efficiency is important, considering sometimes there are many ways to decompose an area, but non all of them are equally easy for calculations. The post-obit picture demonstrates a case of a blended area, that is decomposed to smaller subareas, using three different methods (amidst many others possible). The global axis of rotation is indicated with red dashed line. With method 'a', the number of subareas is 4, with method 'b' it is 5 and and with method 'c', 6.

Figure ii. Three alternative ways to divide the peak-left gray area to subareas, in order to notice its moment of inertia around a horizontal centrality. Which one is more preferable?

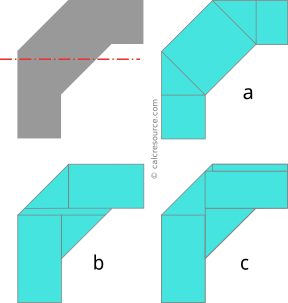
Method 'a' seems more uncomplicated, and employs the least number of subareas, just the calculation of the moment of inertia of the central inclined rectangle is rather difficult. No formula is available for this particular bending of inclination of the rectangle that gives its moment of inertia effectually an axis parallel to the global i. Firstly, we have to find the moments of inertia I_ten and I_y effectually the inclined centroidal axes of the rectangle, and then transform them around a horizontal axis, using the formulas for axis rotation. Surely, it tin can be done this way, but it is not very efficient calculation wise. Methods 'b' and 'c' on the other hand, do not present such a problem. For each one of their subareas, there are hands bachelor analytical formulas, we tin can employ to calculate their moments of inertia around a parallel to global centrality. In particular, method 'b' seems a bit more efficient, since it employs one less subarea, compared to method 'c'.

Sometimes, it is more efficient to define negative subareas, that when subtracted from some other, bigger subarea, produce the total composite shape. Take as an example the rectangular tube in the adjacent figure. Conventionally, it can be decomposed to iv rectangular subareas, one for each of the walls, that added together produce the composite shape (method 'a'). Just a more than efficient method is to define but two rectangular subareas, one for the outer perimeter and one for the inner perimeter (method 'b'). The latter, if subtracted from the former, produces the composite shape and for this reason is characterized as negative subarea. Following this pattern, the moment of inertia of the negative subarea is going to be subtracted from the respective one of the outer perimeter, in gild to find the resulting moment of inertia of the rectangular tube. Autonomously from this, all other steps of the calculation procedure are normally applicative for the negative subarea.

Figure 3. 2 alternative ways to define subareas for the rectangular tube (tiptop-left). Method 'b' utilizes a negative subarea (cutting-out)

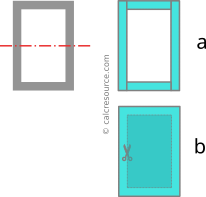
With step 2, we determine the centroid of each subarea, specifically its distance from the global axis. The piece of work we have to do in this stride, depends on the way the subareas have been divers, in the first stride. Simpler subareas, generally require less calculations to detect their centroid, but also the position of subarea, relative to the global axis is important. Visiting again the rectangular tube (Figure 3), if the global axis is a centroidal 1 (passing through middle height of the department), then using method 'b', the centroids of the two rectangular subareas, are located on middle height also, and therefore characteristic null altitude from the global axis. To the contrary, with method 'a', the centroids of top and lesser subareas feature non-zero distance from global axis, which we take to find. Consequently, going with method 'b', not but we avoid whatsoever calculation, but as an additional do good, the work we must practice for step iv (Parallel Axis Theorem) should be less.

With step 3, we calculate the moment of inertia of each subarea effectually the parallel axis passing through its centroid. Commonly, we use bachelor formulas (tables with moments of inertia of common shapes tin exist handy, bank check this one) but if none is bachelor, we have to calculate the definite integral, , over the whole subarea, where variable y is the distance from the axis. Again, the definition of the subareas in step 1, heavily affects the work we have to do here.

With stride 4, nosotros apply the Theorem of Parallel Axes to all subareas, and so that their moments of inertia, go all transferred around the global axis:

where, A_i is the expanse of subarea i, d_i is the distance of subarea i centroid from the global axis (equally adamant in stride two), I_i,c is the moment of inertia of subarea i around its centroid (equally determined in step 3) and I_i,g is the wanted moment of inertia of subarea i around the global centrality.

With stride five, we add all the resulting moments of inertia from previous pace and the final sum is the wanted moment of inertia of the composite area around global axis. If we have any negative subareas defined though, we have to subtract them from the sum. Using a mathematical expression:

where index i indicates a normal (positive) subarea, while index j indicates a negative one.

Note that add-on (or subtraction) of the moments of inertia, I_i,grand , of the multiple subareas, is allowed in this step because all of them are divers around the same centrality of rotation, the global i. That was indeed the purpose of pace 4. To the contrary, nosotros are not immune to practise the same with the moments of inertia from footstep 3, because each one is defined around a unlike parallel axis, passing through the local subarea centroid.

Never add together or subtract moments of inertia defined around different axes!

When all subareas share a convenient common axis

In some cases, it occurs and so that all defined subareas share a common axis of rotation that is convenient to calculate their moments of inertia around. By convenient, it is meant that a) it is parallel to the global axis and b) there are bachelor and piece of cake to calculate formulas for all subareas. It is not necessary a centroidal axis neither identical to the global centrality.

In such cases, it may be preferable to calculate the moments of inertia of the subareas around this convenient centrality. The required steps, with this simplified procedure are outlined like this:

1. Identify simply shaped subareas the composite surface area can be decomposed to.
2. Calculate the moment of inertia of each subarea around the user-friendly centrality.
3. Add together (or subtract for negative subareas, come across examples) the moments of inertia from the last footstep.
4. Use the Theorem of Parallel Axes to find the moment of inertia of the composite shape, around the global centrality

Effigy four. Simplified flowchart, for the adding of the moment of inertia of a composite expanse, when all subareas share a convenient common axis.

With step iii, the moment of inertia of the blended area is found around user-friendly centrality O-O:

where index i indicates a normal (positive) subarea, while index j indicates a negative one.

Addition (or subtraction) of the moments of inertia of multiple subareas is immune because all of them have been found in step 2 around the same axis, the convenient one.

With pace iv, the moment of inertia of the composite area gets transferred, using the Theorem of Parallel Axes, from the convenient axis, to the global centrality:

where d_{one thousand} is the distance of global axis from the composite surface area centroid, d_o is the distance of user-friendly centrality from the composite area centroid, and A is the surface area of composite shape. Of course, if these 2 axes, convenient and global, are ancillary then this stride is redundant and we simply conclude that: . Too, if the global axis is a centroidal 1, so the above expression is simplified to: .

Example i

Calculate the moment of inertia of the shape shown in the post-obit figure, effectually a horizontal axis x-x, passing through centroid. Shape dimensions are: b=15'', h_one=20'', h_ii=10''.

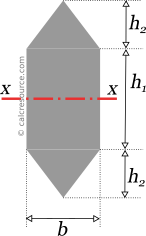
Due to symmetry, the centroid of the composite area is located in the center height of the shape, that is also the middle of superlative h₁ . Since global axis ten-ten (in blood-red color) is passing through centroid, it passes through the middle of h₁ also.

Footstep i

We split up the composite area to smaller subareas equally shown in the following schematic. 3 subareas are defined, one rectangular and two triangular. These volition be referred as, subareas ane,2 and 3, as depicted in the figure.

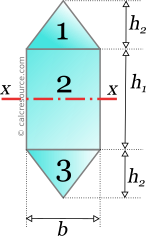
No convenient axis of rotation exists, common to all 3 subareas. Nosotros will continue with the remaining steps of the process (come across Figure 1).

Pace 2

For each subarea, we find the altitude of its centroid from the global axis. Every bit described in the beginning, the global centrality is passing through the middle of h₁ .

For subarea 1, that is a triangle with elevation h_two, the centroid is located, , above the base of operations of the triangle. Therefore, its distance from the global axis is:

For subarea two, that is a rectangle, the centroid is located at the center of its superlative , which coincides with the location of the global axis. Therefore:

For subarea 3, we don't need to make whatsoever adding, since, due to symmetry, it must accept the same distance from global axis, with subarea 1. That is:

The negative sign indicates a position below the axis. Note that the sign of distance is non important, since by definition, it gets squared, and as a result, subareas at either sides of the axis, contribute positively to the moment of inertia.

Pace iii

For each subarea, we notice the moment of inertia around a parallel to x centrality passing through subarea centroid. We apply available formulas from this table.

For subarea i:

For subarea two:

For subarea 3, no calculation is needed, because its shape is identical to that of subarea 1. Therefore:

Step iv

For each subarea we employ the Theorem of Parallel Axes, to discover its moment of inertia effectually global centrality 10-x. We use the distances, , from stride two, and the moments of inertia, , from step 3. We demand the surface area of each subarea likewise, and then we find them first:

At present we utilize the Theorem of Parallel Axes, for each subarea.

For subarea 1:

For subarea ii:

For subarea 3:

Due to symmetry effectually the global axis, the effect for subarea three should not exist different than that of subarea ane:

Step 5

Nosotros add together for all subareas, the moments of inertia from the final step:

This is the wanted moment of inertia of the composite area, around axis x-10.

The following table organizes the adding procedure in a tabular format:

Area	Ic	d	A	Ix=Ic+Adtwo
	(in4)	(in)	(intwo)	(infour)
i	416.67	13.333	75	13750
2	10000	0	300	10000
3	416.67	-13.333	75	13750
Total			450	37500

Instance 2

Calculate the moment of inertia of the shape given in the post-obit figure, around a horizontal centrality ten-x that is passing through centroid. Shape dimensions are: r=20'', a=15'', b=12''. The curved border is a round one. As well, for the needs of this instance, the altitude of the centroid from the base of the shape is given: y_c=8.8083'' .

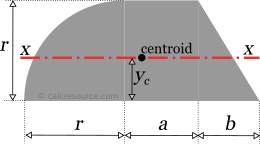
Stride 1

We divide the composite area to smaller subareas as shown in the following figure. Iii subareas are defined, one quarter circle, one rectangle and one correct triangle. These will be referred as, subareas 1,2 and iii, as depicted in the figure.

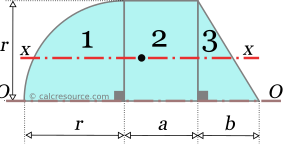
Looking closely to the three subareas, we can recognize that in that location exists a mutual, parallel to x, axis effectually which all three moments of inertia tin can be easily establish: the axis passing form the base of the shape. We name it axis O, and from here on, we volition follow the simpler procedure, which is applicable only when a convenient mutual axis exists for all subareas (see Effigy 4).

Step 2

For each subarea, we detect the moment of inertia effectually the convenient axis O, passing through the base. We use available formulas from this table.

For the quarter round subarea i:

For the subarea 2:

For the subarea 3:

Step iii

We add the moments of inertia around the convenient axis O, for all subareas:

Pace 4

For the total composite expanse, we use the Theorem of Parallel Axes, to discover its moment of inertia around the global axis x-x. Nosotros need the surface area of the blended shape, and so we will observe it offset, through the already defined subareas 1,2 and 3.

Subarea 1: .

Subarea two: .

Subarea iii: .

Total surface area:

Next, the moment of inertia of the composite area around axis O (from step 3) gets transferred, using the Theorem of Parallel Axes, to global axis x, which happens to be a centroidal i too. The theorem takes the form:

where y_c is the distance of the centroid from the base of operations, in other words the distance betwixt the two axes. In our instance it is given, so nosotros may proceed directly to the calculation:

This is the wanted moment of inertia of the composite expanse around axis x-x.

Example iii

Calculate the moment of inertia of the shape given in the following effigy, around a horizontal axis x-x that is passing through centroid. Shape dimensions are: a=25'', b=50'', d=30'' and t=nine''. For the needs of this example, the distance of the centroid from the base of the shape is also given: y_c=19.5''

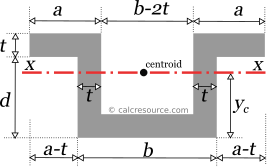
Step 1

The total area is divided to smaller subareas as depicted in the next figure. Iv subareas are defined, all of them rectangular. Subareas 2,iii and four are negative ones, and are subtracted from subarea 1, which surrounds the shape from left to correct and from lesser to height.

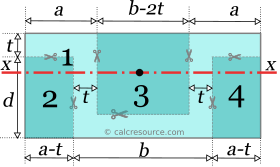
No convenient centrality of rotation is identified, that facilitates the adding of the moments of inertia commonly for all subareas. The standard process will be followed in the side by side steps (as outlined in Figure 1).

Step 2

For each subarea, we discover the distance of its centroid from the global axis. The distance of the global axis from the base is y _c and information technology is given. We have to find the altitude of each subarea centroid from base, and subtract information technology from y_c. The difference shall be the altitude between subarea centroid and the global centrality.

Subarea 1, is a rectangle with height d+t, and its centroid is located at the middle of this height. Therefore, its distance from the global axis is:

Subarea two, is a rectangle, with height d. Therefore:

The negative sign indicates that the centroid lies below the global centrality.

Subarea 3, is as well a rectangle, with pinnacle d, but with an starting time t from base. Thus the distance of its centroid from global axis should be:

For subarea four, we don't need to make a new calculation, since it is similar to subarea 2. Thus:

Step 3

In this step, the moment of inertia of each subarea is calculated, around a parallel to x centrality, passing through its centroid.

For the rectangle of subarea ane, the width is: , and the peak is: . The moment of inertia is:

Subareas 2 and 4, both have width: , and acme: , the moment of inertia is found:

And finally, for subarea 3, the width is: , and the height is: . Its moment of inertia is:

Information technology would be wrong to add together or subtract the moments of inertia nosotros just have found, because each one is related to a dissimilar axis of rotation, passing through the centroid of the corresponding subarea.

Step 4

In this step, the Theorem of Parallel Axes is practical, for each subarea, in order to find its moment of inertia around the global axis x-x, knowing its moment of inertia effectually its centroid. The distances, , from footstep 2, and the moments of inertia, , from step iii will be utilized. Nevertheless, the surface areas are also needed. Without writing again the dimensions of each subarea, from the previous step, the surface areas are found:

Now we apply the Theorem of Parallel Axes, for each subarea.

For subarea ane:

For subarea 2:

For subarea 3:

For subarea iv:

No calculation is needed, due to similarity with subarea ii:

Step 5

In this pace the resulting moments of inertia from the previous step are added together. We are entitled to add or subtract them now, because all have been found around the aforementioned axis, the global i. The negative subareas 2,three and 4, should be subtracted from the sum.

This final reply for the moment of inertia of the composite area around centroidal axis 10-x.

The above adding procedure tin be summarized in a table, like the one shown here:

Surface area	Ic	d	A	Ix=Ic+Advertizing2
	(in4)	(in)	(in2)	(infour)
1	405347	0	3198	405347
two (negative)	36000	-4.v	480	-45720
3 (negative)	72000	4.5	960	-91440
4 (negative)	36000	-4.5	480	-45720
Total			5118	222467

Liked this page? Share it with friends!

Source: https://calcresource.com/moment-of-inertia-compound.html

Share this post